
using the notation |0> for the ground phonon state and |1> for the excited phonon state.
The entanglement to phonons of a single qubit in the 4 qubit system destroys the
adiabatic time development. We introduce a single phonon mode as an additional component
of the many-particle basis states:

using the notation |0> for the ground phonon state and |1> for the excited phonon
state.
The Hamiltonian has an additional term due to the phonon and its interaction with,
for instance, the 3rd qubit:
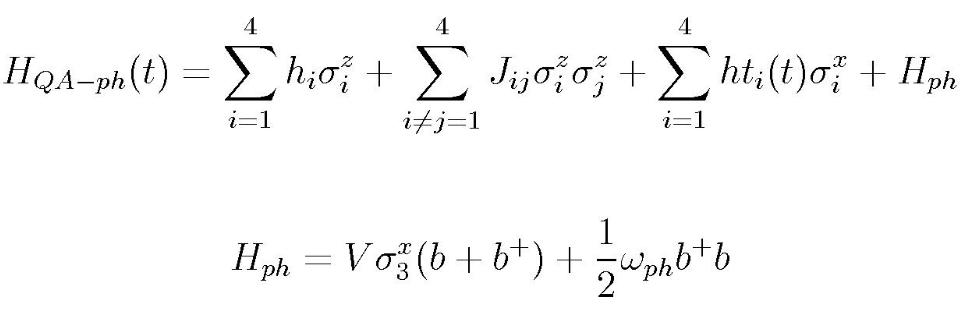
The term H{ph} is analogous to the Jaynes-Cummings Hamiltonian of a two-level atomic
system, coupling to the phonon field with coupling strength V. b^+ and b are
creation and annihilation operators for the phonon mode, \omega{ph}: the phonon
frequency.
The matrix elements are evaluated according to the rules above. For instance some
diagonal matrix elements:
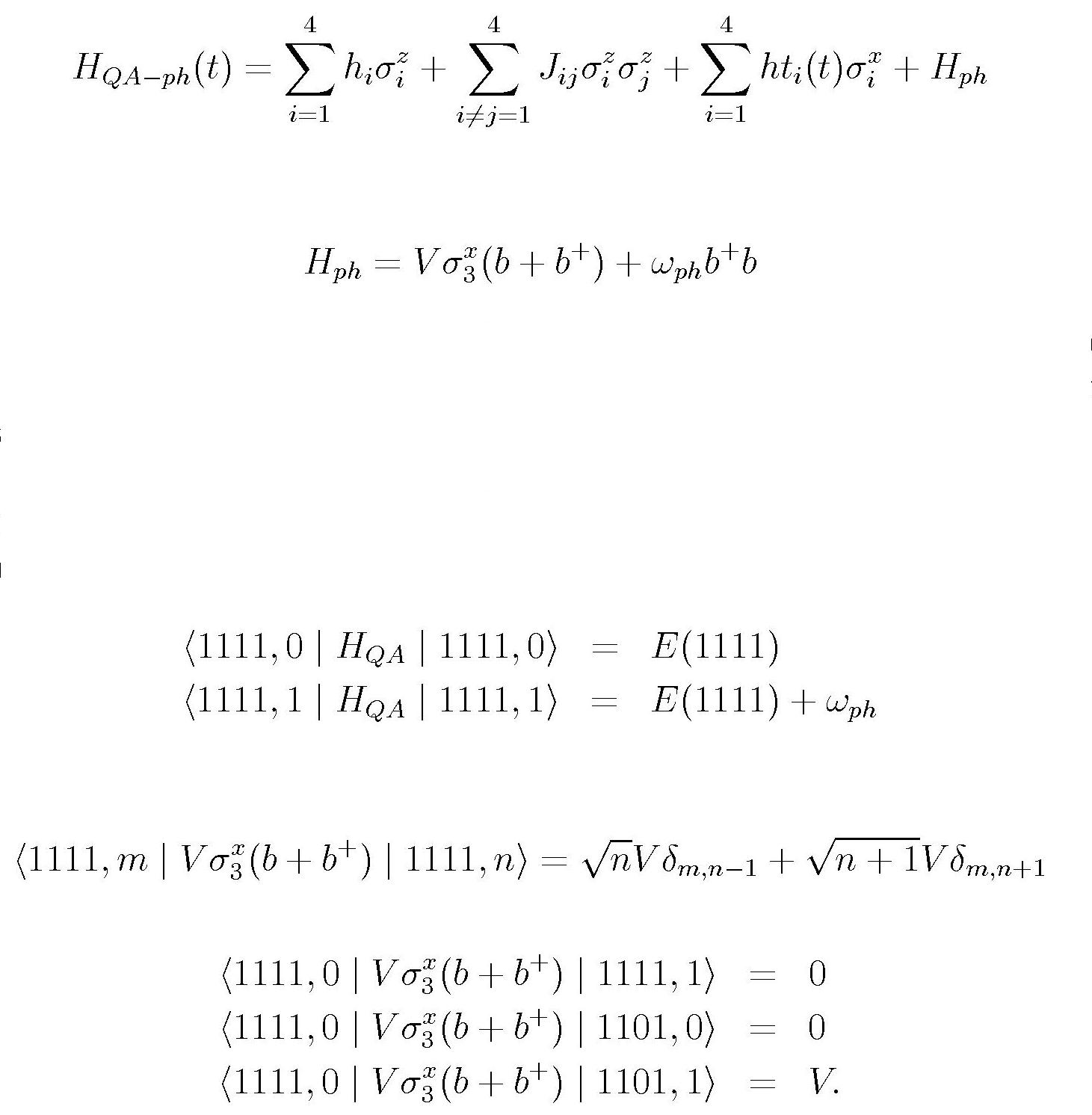
Thus, non-zero off-diagonal matrix elements of the Hamiltonian exist only between
4 qubit basis states with spin flip in the 3rd qubit, accompanied by a change in
the state of the phonon.
The full 32 X 32 configurational matrix looks as follows:

The result of a sudden perturbation of the 4 qubit system by a single phonon mode
is destroyed adiabaticity. Figure \ref{diab-V} shows that a fast entanglement to
the phonon field around t=1000 perturbs the eigenstates dramatically and the system
cannot recover the adiabatic development.
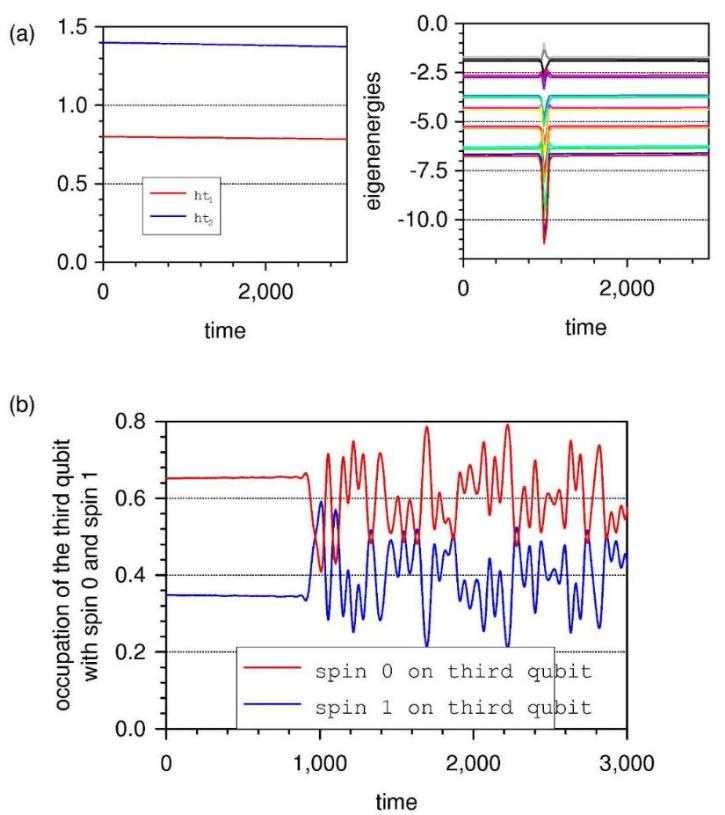
Fig. 10: Destroyed adiabaticity and spin flips in the third qubit as a result of
the fast entanglement to the phonon field. (a) In the upper left plot the variation
with time of the transverse magnetic fields ht1(t) and ht2(t) are shown. The
variation with time of the transverse magnetic fields is so slow that it does not
influence the effect due to the phonon field. On the righthand side the effect
of the sudden switch-on of the interaction with the phonon field on the eigenenergies
of the 4 qubit system is displayed. (b) The development with time of the occupation
summed up over basis states with spin 0 and spin 1 in the third qubit shows
the destroyed adiabaticity and the chaotic occupation of spin 0 and spin 1 states
in the third qubit as a result of the entanglement of the phonon field to this
qubit.
The spin on the third qubit, which is affected by the phonon field, flips completely
arbitrarily after the destroyed adiabaticity, as the lower plot in fig. 10 shows.